Comment évaluer une formule sur Excel : le déroulement pas à pas
Dans ce tutoriel, je vais vous montrer comment utiliser la fonctionnalité d’évaluation de formule sur Excel, qui permet de décomposer le déroulement d’une formule pas-à-pas
Téléchargement
Vous pouvez télécharger le fichier d'exemple de cet article en cliquant sur le lien suivant :
Tutoriel Vidéo
Partie 1 : Comment évaluer une formule sur Excel : le déroulement pas à pas (voir le tutoriel)
Vous trouverez très régulièrement de nouvelles vidéos sur la chaîne, alors pensez à vous abonner pour ne manquer aucune astuce et devenir rapidement un pro d’Excel (cliquez-ici) !
Partie 2 : Utiliser l’outil d’évaluation pour construire des formules complexes sur Excel (SOMMEPROD) (voir le tutoriel)
Vous trouverez très régulièrement de nouvelles vidéos sur la chaîne, alors pensez à vous abonner pour ne manquer aucune astuce et devenir rapidement un pro d’Excel (cliquez-ici) !
1. Présentation (et exemple simple)
Qu’on se le dise, en dehors de quelques rares bugs connus, Excel effectuera toujours les calculs que nous lui demandons ! Lorsqu’un résultat retourné n’est pas celui que nous espérons, cela viendra pratiquement dans tous les cas d’une erreur dans la rédaction des formules.

Tout le monde commet des erreurs, y compris les utilisateurs les plus chevronnés.
L’important dans ce cas-là est d’identifier cette erreur pour la corriger au plus vite.

Et justement, pour y parvenir Excel nous propose un outil extrêmement pratique : il s’agit de l’outil d’évaluation des formules.
2. Exemple d’utilisation de l’évaluation des formules
Pour introduire le fonctionnement de cet outil, nous allons commencer par un exemple très simple :

Dans ce document, qui reprend la synthèse d’exploitation d’une entreprise, nous souhaitons simplement connaître le montant de la marge brute réalisée en Europe.
=B9+B10
Il s’agit de l’opération la plus simple que nous puissions demander à Excel, une simple addition.
Par contre, il peut être intéressant de voir comment Excel procède pour résoudre ce calcul.
Pour cela, nous sélectionnons la cellule qui contient le calcul, puis nous nous rendons dans le menu Formules du ruban et dans le groupe Vérification des formules, nous cliquons sur le bouton Évaluer la formule :

Excel nous présente alors la fenêtre d’Évaluation des formules :

Dans celle-ci, nous retrouvons dans le cadre blanc la formule de la cellule sélectionnée, ainsi que les coordonnées de celles-ci juste avant.
Dans la formule, nous retrouvons un terme souligné (B9). Il s’agit du premier élément qu’Excel va calculer.
Un clic sur le bouton Évaluer permet de remplacer la référence à cette formule par sa valeur :

Ensuite, Excel souligne le second élément afin de pouvoir effectuer exactement la même opération :

Nous constatons au passage que le montant des achats de marchandises vendues est repris en négatif, exactement de la même manière que nous le retrouvons exprimé dans le tableau.
Et pour finir, l’ensemble des valeurs numériques sont maintenant soulignées, ce qui signifie qu’Excel va effectuer le dernier calcul pour obtenir le résultat attendu, c’est-à-dire effectuer la somme des deux valeurs :

Pour revisionner le détail du calcul, nous pouvons alors cliquer sur le bouton Redémarrer.
3. Afficher la résolution pas à pas
Lorsque le résultat d’une cellule dépend d’un calcul (simple référence à une autre cellule, ou calcul complexe), il est possible de remonter tout à l’origine.
Pour cela attardons nous sur le résultat net de l’entreprise :
- Nous sélectionnons la cellule :

- Puis nous lançons l’outil d’évaluation de la formule :

Ici nous comprenons bien que la formule consiste ici encore en une simple addition.
En revanche, si nous analysons le document, nous constatons que la première cellule insérée dans cette addition (la cellule E16) correspond à l’EBE réalisé au niveau mondial, et il s’agit donc d’un calcul.
Lorsque nous cliquons sur Pas à pas détaillé, Excel va donc nous détailler le processus de résolution de cette cellule dans un nouveau cadre :

La référence à la cellule E16 passe alors en bleu et nous retrouvons l’évaluation de son résultat en dessous.

Ainsi il est possible de redescendre jusque trois niveaux au total.
Ensuite, il suffit de cliquer sur le bouton Évaluer pour obtenir le résultat de la cellule E14 :

Un clic sur le bouton Pas à pas sortant permet de remonter d’un niveau :

4. Évaluer une formule complexe
Pour ce nouvel exemple, nous souhaitons obtenir le montant d’un poste en fonction d’un pays donné.

Le poste et la zone sont sélectionnés à partir d’une liste déroulante simple. Pour savoir comment insérer une liste déroulante dans une feuille de calcul, suivez ce tutoriel.

Ensuite nous utilisons une formule SOMMEPROD() pour obtenir le résultat désiré :
=SOMMEPROD((A9:A18=B24)*(B8:E8=B25)*B9:E18)
L’outil d’évaluation de formule est le complément parfait pour bien appréhender le fonctionnement de cette formule relativement complexe à appréhender :

Nous pouvons donc commencer évaluer cette formule, nous voyons déjà qu’Excel va commencer par récupérer la valeur de la cellule B24 dans laquelle se trouve le poste pour lequel nous souhaitons obtenir le détail (dans notre exemple, il s’agit du poste « Frais pays »).
Un second appui permet de remplacer les valeurs contenues dans la plage de cellules située aux coordonnées A9 à A18 :

Comme nous pouvons le constater sur la capture ci-dessus, les valeurs correspondantes sont saisies sous la forme d’une liste dans laquelle chaque élément est séparé par un point-virgule, et tous les éléments sont encadrés par des accolades.
Dans Excel, ces accolades permettent d’identifier une matrice, c’est-à-dire un tableau de données qui peut être composé de plusieurs lignes et colonnes et sur lequel il est possible d’effectuer des opérations. Chaque point-virgule représente une nouvelle ligne de cette matrice, et chaque virgule simple entre deux éléments représente quant à elle une nouvelle colonne.
À cette étape de la résolution de la formule, nous observons que chaque élément est séparé par un point-virgule et il n’y a aucun point. Nous pouvons donc en déduire que la matrice stockée dans la mémoire d’Excel est une matrice verticale de dimension 10x1 (1 lignes et une seule colonne).

Dans l’étape suivante, Excel passe en revu chaque élément de cette matrice pour le comparer avec la valeur de la cellule B24. Lorsque ces deux valeurs sont équivalentes, alors Excel affecte la valeur booléenne (c’est-à-dire qui peut être également à VRAI ou à FAUX) à cet élément.
Ainsi, nous nous retrouvons avec une nouvelle matrice composée uniquement de VRAI et de FAUX (cette matrice a toujours une dimension de 10x1).
Cela étant fait, Excel effectue le même test pour déterminer quel pays est sélectionné (valeur de la cellule B25 : « ASIE ») :

Ici nous constatons que les éléments sont séparés, non plus par des points-virgules comme nous venons juste de le voir dans la matrice précédente, mais par des virgules.
Cela signifie que cette matrice a pour dimension 1x4.
Ensuite Excel compare les éléments de la matrice avec la valeur de la cellule B25 (« ASIE ») afin de remplacer les valeurs de la matrice par des VRAI ou des FAUX :

Ensuite, et c’est là l’opération la plus complexe Excel va multiplier les deux matrices ensemble pour n’en former qu’une de dimension 10x4 !

Sachant que dans cette opération, un résultat « FAUX » équivaut à 0, tandis que « VRAI » équivaut à 1 :

Ensuite, il suffit de multiplier chaque élément de la première matrice en colonne par les éléments de la second, cette fois-ci en ligne, afin d’obtenir une matrice en deux dimensions :

Nous obtenons ainsi une matrice de dimension 4x10 composée de 0 et de 1.

Pour terminer, nous pouvons maintenant multiplier chacun des éléments avec l’éléments situé à la même position de la matrice représenté par la plage des cellules ayant pour coordonnées B9 jusqu’à E18 :
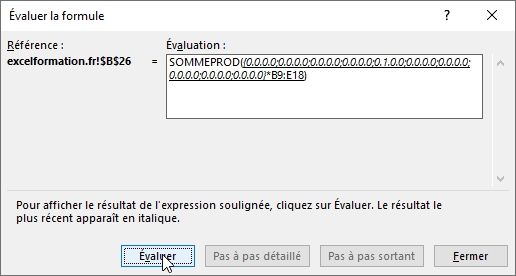
Évidemment, chaque élément multiplié par 0 est égal à 0 et chaque élément multiplié par 1, vaut la valeur de celui-ci :


Et pour finir la dernière opération consiste à effectuer la somme de la valeur de chacun de ces éléments pris indépendamment les uns des autres :
(Facile, il ne reste qu’un seul élément différent de zéro !)

Article initialement publié le 13 août 2019, puis modifié le 12 septembre 2019
